Гравитационное поле

Гравитацио́нное по́ле, или по́ле тяготе́ния, — фундаментальное физическое поле, через которое осуществляется гравитационное взаимодействие между всеми материальными телами.

Гравитационное поле в классической физике

Закон всемирного тяготения Ньютона

Закон тяготения Ньютона

Основная статья: Классическая теория тяготения Ньютона

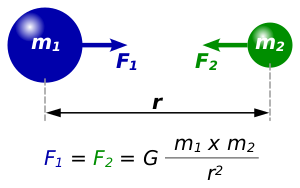
В рамках классической физики гравитационное взаимодействие описывается «законом всемирного тяготения» Ньютона, согласно которому сила гравитационного притяжения между двумя материальными точками с массами [math]\displaystyle{ m_1 }[/math] и [math]\displaystyle{ m_2 }[/math] пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними:

[math]\displaystyle{ F=G\frac{m_1 m_2}{r^2}. }[/math]

Здесь [math]\displaystyle{ G }[/math] — гравитационная постоянная, приблизительно равная [math]\displaystyle{ 6{,}673 \cdot 10^{-11} }[/math] м³/(кг с²), [math]\displaystyle{ r }[/math] — расстояние между точками.

Решение задачи динамики в общем случае, когда тяготеющие массы нельзя считать материальными точками, подразделяется на два этапа: вначале рассчитывается гравитационное поле, создаваемое этими массами, а затем определяется его действие на массивные тела в изучаемой системе.

Расчёт гравитационного потенциала

Основная статья: Гравитационный потенциал

Гравитационное поле является потенциальным. Его потенциал [math]\displaystyle{ \varphi(\mathbf r) }[/math] удовлетворяет уравнению Пуассона:

[math]\displaystyle{ \Delta \varphi(\mathbf r) = -4 \pi G \rho(\mathbf r) }[/math],

где [math]\displaystyle{ \Delta }[/math] — оператор Лапласа. Решение данного уравнения имеет вид:

[math]\displaystyle{ \varphi(\mathbf r) = -G \int_{V^\prime}\frac{\rho(\mathbf r^\prime)dV^\prime}{|\mathbf r-\mathbf r^\prime|} }[/math].

Здесь [math]\displaystyle{ \mathbf r }[/math] — радиус-вектор точки, в которой определяется потенциал, [math]\displaystyle{ \mathbf r^\prime }[/math] — радиус-вектор элемента объёма [math]\displaystyle{ dV^\prime }[/math] c плотностью вещества [math]\displaystyle{ \rho(\mathbf r^\prime) }[/math], а интегрирование охватывает все такие элементы. На бесконечности [math]\displaystyle{ \varphi = 0 }[/math].

В частном случае поля, создаваемого расположенной в начале координат точечной массой [math]\displaystyle{ M }[/math], потенциал равен

[math]\displaystyle{ \varphi(\mathbf r) = -G \frac{M}{r} }[/math].

Этим же выражением описывается потенциал тела со сферически-симметрично распределённой массой [math]\displaystyle{ M }[/math], за его пределами.

В общем случае тела произвольной формы на больших расстояниях от него неплохое приближение для потенциала даёт формула:

[math]\displaystyle{ \varphi(\mathbf r) = -G\left( \frac{M}{r}+\frac{A+B+C-3I}{2r^3}\right), }[/math]

где за начало координат принят центр масс тела, [math]\displaystyle{ A, B, C }[/math] — главные моменты инерции тела, [math]\displaystyle{ I }[/math] — момент инерции относительно оси [math]\displaystyle{ \mathbf r }[/math]. Эта формула несколько упрощается для астрономических объектов, представляющих собой сплюснутые сфероиды вращения с концентрически однородным распределением масс. У таких тел [math]\displaystyle{ A=B }[/math] и [math]\displaystyle{ I=A+(C-A)\sin^2\alpha, }[/math] где [math]\displaystyle{ \alpha }[/math] — угол между [math]\displaystyle{ \mathbf r }[/math] и плоскостью главных осей [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math]. В итоге

[math]\displaystyle{ \varphi(\mathbf r) = -G\left( \frac{M}{r}+\frac{C-A}{2r^3}(1-3\sin^2\alpha)\right). }[/math]

Движение в гравитационном поле

Если потенциал поля определён, то сила притяжения, действующая в гравитационном поле на материальную точку с массой [math]\displaystyle{ m }[/math], находится по формуле:

[math]\displaystyle{ \mathbf F(\mathbf r) = - m \nabla \varphi(\mathbf r) = -Gm \int_{V^\prime}\frac{\rho(\mathbf r^\prime)(\mathbf r-\mathbf r^\prime)dV^\prime}{|\mathbf r-\mathbf r^\prime|^3} }[/math].

В частном случае поля точечной массы [math]\displaystyle{ M }[/math], расположенной в начале координат ([math]\displaystyle{ \mathbf r^\prime = \mathbf 0 }[/math]), действующая сила составит

[math]\displaystyle{ \mathbf F(\mathbf r) = - G\,\frac{mM}{r^3}\,\mathbf r }[/math].

Траектория материальной точки в гравитационном поле, создаваемом много большей по массе материальной точкой, подчиняется законам Кеплера. В частности, планеты и кометы в Солнечной системе движутся по эллипсам или гиперболам. Влияние других планет, искажающее эту картину, можно учесть с помощью теории возмущений.

Если исследуемое тело нельзя рассматривать как материальную точку, то его движение в гравитационном поле включает также вращение вокруг оси, проходящей через центр масс:

[math]\displaystyle{ \frac{d \mathbf H}{dt} = \mathbf K. }[/math]

Здесь: [math]\displaystyle{ \mathbf H }[/math] — угловой момент относительно центра масс, [math]\displaystyle{ \mathbf K }[/math] — равнодействующая моментов действующих сил относительно центра масс. Более общий случай, когда масса исследуемого тела сравнима с массой источника поля, известен как задача двух тел, и её формулировка сводится к системе двух независимых движений. Исследование движения более чем двух тел («задача трёх тел») разрешимо только в нескольких специальных случаях.

Недостатки ньютоновской модели тяготения

Практика показала, что классический закон всемирного тяготения позволяет с огромной точностью объяснить и предсказать движения небесных тел. Однако ньютоновская теория содержала ряд серьёзных недостатков. Главный из них — необъяснимое дальнодействие: сила притяжения передавалась неизвестно как через совершенно пустое пространство, причём бесконечно быстро. По существу ньютоновская модель была чисто математической, без какого-либо физического содержания. Кроме того, если Вселенная, как тогда предполагали, евклидова и бесконечна, и при этом средняя плотность вещества в ней ненулевая, то возникает гравитационный парадокс: потенциал поля всюду обращается в бесконечность. В конце XIX века обнаружилась ещё одна проблема: заметное расхождение теоретического и наблюдаемого смещения перигелия Меркурия.

На протяжении более двухсот лет после Ньютона физики предлагали различные пути усовершенствования ньютоновской теории тяготения. Эти усилия увенчались успехом в 1915 году, с созданием общей теории относительности Эйнштейна, в которой все указанные трудности были преодолены. Теория Ньютона оказалась приближением более общей теории, применимым при выполнении двух условий:

1. Гравитационный потенциал в исследуемой системе не слишком велик (много меньше [math]\displaystyle{ c^2 }[/math]). В Солнечной системе это условие для большинства движений небесных тел можно считать выполненным — даже на поверхности Солнца отношение [math]\displaystyle{ |\varphi| / c^2 }[/math] составляет всего [math]\displaystyle{ 2{,}12 \cdot 10^{-6} }[/math]. Заметным релятивистским эффектом является только указанное выше смещение перигелия.
2. Скорости движения в этой системе незначительны по сравнению со скоростью света.

Гравитационное поле в общей теории относительности

Основная статья: Общая теория относительности

В общей теории относительности (ОТО) гравитационное поле является не отдельным физическим понятием, а свойством пространства-времени, появляющимся в присутствии материи. Этим свойством является неевклидовость метрики (геометрии) пространства-времени, и материальным носителем тяготения является пространство-время. Тот факт, что гравитацию можно рассматривать как проявление свойств геометрии четырёхмерного неевклидова пространства, без привлечения дополнительных понятий, есть следствие того, что все тела в поле тяготения получают одинаковое ускорение («принцип эквивалентности» Эйнштейна). Пространство-время при таком подходе приобретает физические атрибуты, которые влияют на физические объекты и сами зависят от них.

Пространство-время ОТО представляет собой псевдориманово многообразие с переменной метрикой. Причиной искривления пространства-времени является присутствие материи, и чем больше её энергия, тем искривление сильнее. В ОТО символы Кристоффеля играют роль гравитационного силового поля, а метрический тензор играет роль гравитационного потенциала. Для определения метрики пространства-времени при известном распределении материи надо решить уравнения Эйнштейна. Ньютоновская же теория тяготения представляет собой приближение ОТО, которое получается, если учитывать только «искривление времени», то есть изменение временно́й компоненты метрики, [math]\displaystyle{ g_{00} }[/math] (пространство в этом приближении евклидово). Распространение возмущений гравитации, то есть изменений метрики при движении тяготеющих масс, происходит с конечной скоростью, и дальнодействие в ОТО отсутствует.

Другие существенные отличия гравитационного поля ОТО от ньютоновского: возможность нетривиальной топологии пространства, особых точек, гравитационные волны.

См. также

• Уравнение Кеплера
• Гравитационная задача N тел
• Задача Кеплера в общей теории относительности

Литература

• Дубошин Г. Н. . Небесная механика. Основные задачи и методы. — М.: Наука, 1968. — 800 с.
• Иваненко Д. Д., Сарданашвили Г. А. . Гравитация. — 3-е изд. — М.: УРСС, 2008. — 200 с.
• Мензел Д. (ред.). Основные формулы физики. Глава 29. Небесная механика. — М.: Изд. иностранной литературы, 1957. — 658 с.
• Мизнер Ч., Торн К., Уилер Дж. Гравитация. — М.: Мир, 1977.

Ссылки

• Тюлина И. А. Об основах ньютоновой механики (к трёхсотлетию «Начал» Ньютона) // История и методология естественных наук. — М.: МГУ, 1989. — Вып. 36. — С. 184—196..